
前回の記事でベルの功績を分かりやすく説明してほしいというご希望をいただきました。今回はそれにチャレンジしてみます。
アインシュタインたちが量子力学を否定するために導いたEPR相関が、実は本当に起きていることを証明したのが、ジョン・スチュワート・ベルという科学者です。それは現在「ベルの定理」と呼ばれています。
ある思考実験
全く数式を使わずにベルの定理を説明することは無理ですので、ごく単純な数式は使わせていただきます。従って、説明は少々長くなります。しかし、古典物理学と現代物理学の論争に決着を付けた、極めて重要なこの定理をご理解いただくためにも、しばらくの間ご辛抱ください。
ベルの定理の重要な部分は、ある思考実験(実際の実験ではなく、考える実験)から引き出されています。
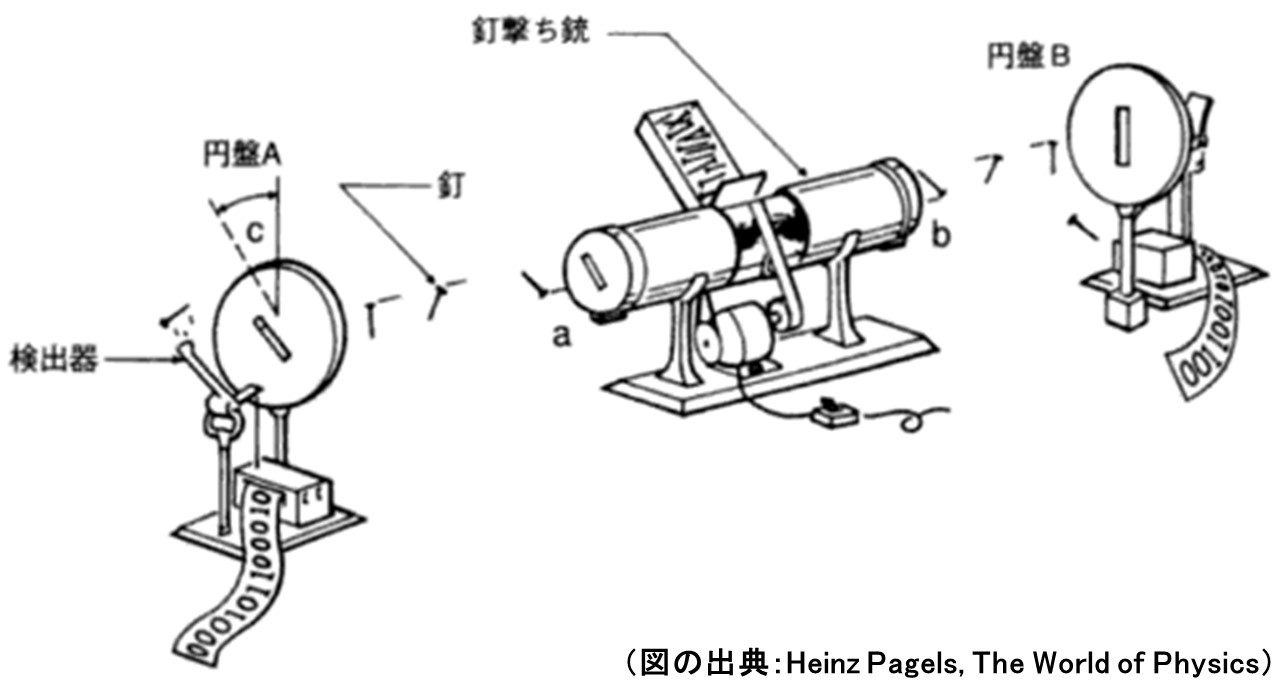
図のような仮想的な実験装置、釘撃ち銃を考えます。この装置は、充填された釘を同時に2本、発射口a、bから横向きに撃ち出すものです。発射口a、bの発射角度が固定されておらず、釘を撃ち出す角度はランダムに変化します。つまり釘は、地面に対して水平の姿勢で飛ぶこともあれば、垂直の姿勢で飛ぶこともあるわけです。ただし、どんな場合でもaとbの角度にズレはなく、同時に飛び出す一対の釘の角度は完全に一致しているとします。
発射口の行く手には、円盤A、Bが置かれています。この円盤には、ちょうど釘が通るくらいのスリット(細長い切り口)が開けられています。そして、飛んできた釘がうまくこのスリットを抜けると、背後の検知器が「1」とカウントします。通り抜けなかった場合には「0」をカウントするとします。
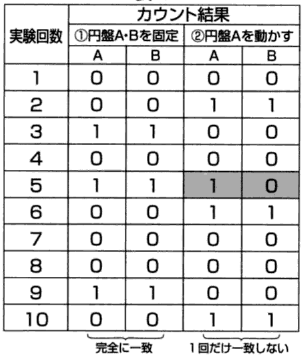 実験です。まず、円盤AとBのスリットの向きを完全に一致させます。飛び出す釘は毎回ランダムな角度に変化しますが、一対の釘の向きは変わりません。
実験です。まず、円盤AとBのスリットの向きを完全に一致させます。飛び出す釘は毎回ランダムな角度に変化しますが、一対の釘の向きは変わりません。
この場合、もしaから発射された釘が円盤Aのスリットを通り抜ければ、bから発射された釘も円盤Bのスリットを通り抜けるはずです。逆にどちらか一方が通り抜けなければ、他方も通り抜けないはずです。従ってカウントの結果は、表の①のように完全に一致します。
次に、円盤Bをそのまま固定して、円盤Aを角度cの範囲内でランダムに動かします。円盤Aと円盤Bのスリットの向きが一致しないことがあるというわけです。従って、今度は一対の釘のうち、どちらか一方が通過し、他方が通過しないということが、何回か発生するでしょう。カウントの結果は、例えば表の②のようになります。
固定していた円盤Bを基準にすれば、Bのカウントに一致しなかったAのカウントは「誤差」といえます。この例では、10回の実験で1回の誤差が発生していますから、誤差は10%、つまり0.1となります。もちろん実際には、10回だけではなく、何千回、何万回の実験を繰り返して誤差を求めます。この10回というのは、あくまでも話を分かりやすくするためのものです。
さて、「角度cのときの誤差が0.1」ということを数式であらわすと、次のようになります。
E(c) = 0.1
逆に円盤Aを固定して、円盤Bを角度cの範囲内でランダムに動かしても、全く同じ誤差が発生するはずです。
では、円盤Aと円盤Bの両方とも、角度cの範囲内でランダムに動かしたら、結果はどうなるでしょうか? 両者ともc動くので、角度は合わせて2c、つまりcの2倍です。この場合の誤差をE(2c)と書きます。
単純に考えれば、E(2c)は、円盤Aの誤差E(c)と、円盤Bの誤差E(c)の和であるように思えます。すなわち、
E(2c) = E(c)+E(c) = 2E(c)
となるはずです。
しかしよく考えると、この推測は正しくないことが分かります。なぜなら、今度の場合、円盤Aも円盤Bも固定しておらず、共に動いているからです。つまり、固定している円盤がないので、誤差の基準が失われているのです。
釘が両方のスリットを通過すれば、一見誤差がないように思いますが、基準が失われているために「両方通過したこと自体が誤差だった」かもしれない、という可能性も考慮しなければならないのです。これを二重誤差といいます。
つまりこの場合、実験全体の誤差E(2c)は、二重誤差が含まれるので(本当は誤差なのに、両方通過してしまい、見かけ上、誤差がないように観測されるので)、先ほどの推測、2E(c)よりも少なめになるはずです。これを式で書けば、次のようになります。
E(2c) ≦ 2E(c)
これをベルの不等式といいます。
ベルの不等式が成立しない!
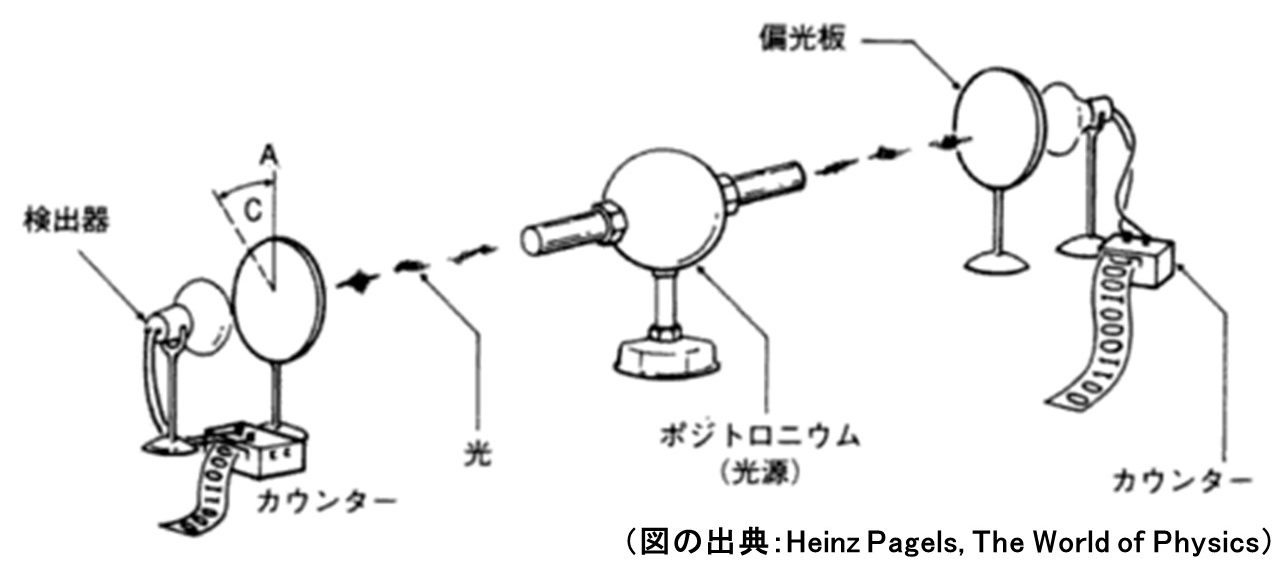
釘を使って行った思考実験を、実際の実験で行います。ポジトロニウムという粒子は、100万分の1秒で崩壊し、一対の光を放出します。このときの一対の光は、偏極(波が揺れる方向)が同じです。つまり先ほどの釘に当たります。
円盤の代わりには、偏光板を用います。偏光板とは、ある方向に揺れる光しか通さないものです。サングラスなどが、この偏光板を利用して作られています。これが先ほどのスリットに当たります。
このような仕組みの装置で実験すると、角度cが30°のときの誤差は、25%になりました。ということは、ベルの不等式に従うと角度2c(2×30°=60°)における誤差は、50%(2×25%)より小さくなるはずです。しかし実際には、60°のときの誤差は75%になってしまいした。つまり、50%より大きくなってしまい、ベルの不等式が成立しなかったのです!
実は、ベルはこの実験をする前に、既にベルの不等式が成立しないことを計算で示していました。それが実験によって証明されたということです。
ベルの不等式が成立しないということは、最初はあまり話題にもなりませんでした。しかしその後、問題の大きさが認識されにつれ、さまざまな研究者が同様の実験を行いました。そして、ベルの不等式が成立しないことが、正式に確認されることとなったのです。
このことは一体、何を意味するのでしょうか? 実はこの実験は、次の2つの事柄を暗黙の前提としていたのです。
1 円盤A、B(偏光板)のどちらを回転させても、他方に影響を及ぼさない。
2 釘(光)は、観測者から影響を受けない。
まず1の前提は当然のように思われます。片方の円盤を回転させたら、何のつながりもない他方の円盤に、その影響が及ぶなどとは、ちょっと考えられません。なぜなら、「わが家の窓が割れたら、100キロメートル離れたあなたの家の窓も割れる」といっているのと同じだからです。
2については、古典物理学が前提としていることです。現代物理学、すなわち量子力学ではこれを前提にしていないことは、先に述べた通りです。しかし一般的に、つまり皆さんの常識としては、「私が物を見たら、その物が動き出す」などとは考えないのが普通でしょう。
要するにこの実験は、ぼくらの日常的な常識を前提にしており、それ以外の特別な前提があったわけではありません。つまりベルの不等式は、そうした常識の産物だったのです。それにもかかわらず、ベルの不等式が成立しないということは、常識の産物が通用しないということです。つまり先の2つの前提のうち、いずれか1つ、あるいは双方に誤りがあることになるのです。「少なくとも1つ、あなたの常識を消してください」ということです。
これは一般的に次のように書き換えられています。これがベルの定理です。
1 非局所作用は存在しない。
2 全ての物事は、観測者の影響を受けない。
この2つのうち、少なくとも1つを否定しなければならない。
ベルの定理によってもたらされた衝撃的な結末
非局所作用とは、どのようなものでしょうか? これを知るには、まず局所作用について理解しなければなりません。局所作用の本質は「接触している」ということです。例えば2つの物体が直接、もしくは何かを介して互いに接触しているとき、両者は「局所的に作用し合っている」といいます。
例えば、ぼくらが物を見る場合も、光を介してその物と接触するわけですから、やはり局所作用です。光は宇宙で最も速い信号であり、その速度は秒速30万km。1秒間に地球を7周半するスピードです。そんなに速い光でも、太陽から地球に届くまでには、8分かかります。つまりぼくらは、いつも8分前の太陽を見ていることになります。このように、局所作用が伝わるには時間がかかるのです。
この「何かが伝わるには時間がかかる」という考え、すなわち局所作用というものは、実は物理学の基本中の基本なのです。なぜなら、AからBへ何かが伝わるのに時間を要するということは、AとBの間に、距離すなわち空間があることになるからです。時間と空間、これこそ自然現象を語る上で、なくてならないものなのです。
では、非局所作用とは何でしょうか? 簡単にいえば、瞬間的に伝わる作用、すなわちテレパシーのようなものです。「非局所作用が存在する」とすれば、今現在の太陽の様子を、今すぐ知ることができるのです。つまり、非局所作用とは「光の速度より速い作用」ということです。
もし、この非局所作用があるとすれば、この広大な宇宙のどことでも、瞬間的に接触することが可能となります。例えば、地球からアンドロメダ星雲という銀河までは、光でも230万年かかる距離ですが、非局所作用があれば一瞬で交信可能だというわけです。これはすなわち、ぼくらは宇宙のあらゆる存在と「一体である」ということと同じなのです。つまり両者の間に空間があるとはいい難くなります。むしろ、「ぼくらは宇宙であり、宇宙はぼくらである」という、区別の付かない存在となるのです。
デビット・ボームという科学者は、「もし非局所作用があるとするなら、あなたの指先の中にアンドロメダ星雲を見ることができる」と表現しています。
しかもアインシュタインの相対性理論を解いていくと、光より速く走るものは時間を逆行する、つまり未来から過去に走るということまで、導かれるのです。
映画『スーパーマン』(1978年)のラスト・シーンも、この理論に基づいています。スーパーマンが恋心を抱いている女性が、巨大地震によって生じた地割れに、車ごと飲み込まれて死んでしまいます。助けにきたが間に合わなかったスーパーマンは、地球の周りをものすごいスピードで飛び始めます。すると、地球が逆回転をし始めます。しばらく飛んでから、再び地上に戻ったスーパーマンは、巨大地震が起きる前の彼女と出会い、無事に命を救った・・・という話です。
つまりスーパーマンは、光の速度より速く飛んだのです。ですから彼は、過去に戻れたのです。あの映画は、ちゃんと相対性理論に基づいて作られていたのです(余談でした)。
このように、もし光の速度より速く飛ぶことができる乗り物が開発されれば、その乗り物はタイムマンシンになります。しかしそんなに速く飛ぶと、人間の体がその力に耐えられませんから、この乗り物に人間が乗ることは、現実的には不可能です。しかしタイムマシンが不可能でも、もし光の速度より速い作用があれば、その作用を利用して未来をあらかじめ知ることは可能です。つまり、予言や予知能力といったものも説明できる可能性を認めざるを得なくなるのです。
もう一度、ベルの定理に戻って見ましょう。
1 非局所作用は存在しない。
2 全ての物事は、観測者の影響を受けない。
この2つのうち、少なくとも1つを否定しなければならない。
古典物理学は、「物事は観測者に影響されない」という立場ですから、「2を肯定」しています。従って、ベルの定理により、「1を否定」しなければなりません。先ほどの実験でいえば、「釘(光)は、実験中たえず、観測者(人間)に影響を受けずに存在している」という立場なので、「円盤A、B(偏光板)は非局所作用によって、互いに影響を及ぼし合っている」となるわけです。
つまり、テレパシーや予知能力のような非局所作用の存在を認めることになるのです。「物事は観測者に影響されない」という立場を取っていたアインシュタインは、その立場故に量子力学を否定するために導いたEPR相関(非局所作用)を認めざるを得なくなってしまうのです。
現代物理学(量子力学)では「物事は観測者に影響される」、すなわち「2を否定」していますから、1を否定する必要はありません。「円盤A、B(偏光板)は、どちらを回転させても相手に影響を及ぼさない」となるわけです。つまり、非局所作用の存在を認めなくてもよいわけです。多くの科学者は、これにより現代物理学に軍配をあげました。
しかし、ベルの定理では「少なくとも1つを否定する」とあるのです。ですから、2つとも否定しても良いわけです。すなわち、現代物理学の立場でも、1を否定できるわけです。
つまり、ベルの定理によって次のような判決が下されたのです。
科学では、テレパシー、予知能力、ぼくらが宇宙の全存在と一体となっている、ということなどを意味する非局所作用を、完全に否定することができない。
これがベルの定理によってもたらされた衝撃的な結末です。
その後、実際に実験で非局所作用(EPR相関)が起きていることが証明されていきました。その話も面白いのですが、また気が向いたときにでも。
>これがベルの定理によってもたらされた衝撃的な結末です。
最後の一文が、このことの重大さを物語っているのでしょうね。
わかりやすい解説をありがとうございます。
>テレパシー、予知能力、ぼくらが宇宙の全存在と一体となっている、ということなどを意味する非局所作用
思い とか 祈り というものは通じるものなのですね。
ピンバック: 夢の量子コンピューター – ∂世界/∂x = 感動