
過去最大の素数が発見されました! 理系人間のぼくとしてはワクワクものです。「素数ってなんだ。俺の生活には関係ねえ」と言う人もいるかもしれないので、ちょっと解説してみます。まずは、報道された内容をご覧ください。
米セントラルミズーリ大は21日、1とその数自身以外では割りきれない素数を研究している同大のカーチス・クーパー教授(計算機科学)が、過去最大となる約2233万桁の素数を発見したと発表した。これまでより約500万桁大きい。
素数は無限に存在することが証明されているが、どのように出現するかは現在もわかっていない。素数は電子商取引などで使われる暗号に応用されている。大きな素数の発見は、より解読が困難な暗号の作製につながり、コンピューターによる計算技術の向上にも役立つと期待される。
これを読んでも「なんじゃらほい」と感じる方が多いかもしれません。もう少しかみ砕いて説明してみましょう。
素数って何?
素数とは、記事に書いてあるとおり、1とその数自身以外では割り切れない数です。「数」とサラリと流していますが、厳密にいうと単なる「数」ではなく、「自然数」です。自然数とは、1、2、3、4、5・・・と、数を数えるときに使うものです。少数点以下がない数です。
例えば、2は素数です。1と2(その数自身)でしか割り切れません。3も素数です。でも、4は素数ではありません。1と4(その数自身)以外に、2でも割り切れます。
ちなみに、1は素数ではありません。「1も、1とその数自身(この場合1は)でしか割り切れないだから、素数じゃないか」と突っ込まれた方は、数学的センスがあります。素晴らしい(拍手)。でも1は素数ではないのです。それを説明するには「素因数分解の一意性」というものを知らないといけないのですが、長くなるのでその詳しい説明は割愛いたします。ともかく、1は素数ではないとご理解ください。
コンピューターでも苦戦する素因数分解

記事に「素数は電子商取引などで使われる暗号に応用されている」と書かれているとおり、現代社会は素数の特徴を利用してセキュリティーがなされています。特にインターネットは、情報の流出には弱いです。それはインターネットの仕組み上、当然のことです。あちらこちらに回線がつながっているのですから、基本的にインターネットを利用する情報は全て公開されていることに等しいです。
例えば、ぼくからあなたへメールを送るときにも、ダイレクトに届けられるわけでありません。途中で幾つかのサーバーを経由しています。その途中のサーバーに悪意があろうがなかろうが、ぼくのメール内容はそこを通っているわけですから、盗み読みされる可能性はあるわけです。
それを防ぐために、こういったインターネット上のやり取りではRSA暗号というものが用いられています。ちなみにRSAとは、この暗号の発明者であるリベスト、シャミア、エーデルマンという3名の頭文字をつなげたものです。RSA暗号をごくごく簡単に説明すると、こんな感じになります。
例えば、23と31は素数です。この2つを掛け算してみます。
電卓があれば簡単に計算できます。では、素因数分解はどうでしょうか。素因数分解とは、「ある数を素数の掛け算にする」ということです。つまり、上の713の素因分解はこうなります。
「なんだ、当たり前じゃないか」と言うかもしれません。それは、最初に掛け算を見て、知っているからです。もしそれを知らずに、「713を素因数分解せよ」と言われたら、結構大変だと思います。「そんなことはないよ」という方は、次の数を素因数分解してみてください。

(スペースが狭いので2行にしていますが、実際は1行に連なる1つの数字)
どうですか? 無理でしょう。ちなみに答えは、こうです。
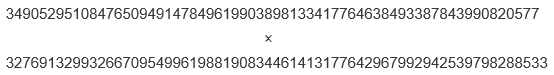
掛け算されている2つの数は、もちろん素数です。これでも十分長い素数ですが、今回発見された素数は、これをはるかに超える約2233万桁という大きさなのです。このブログの文字の大きさで数字を書いていったら、2行どころの話ではなく、A4判の紙で1万枚以上になるほど、とてつもなく大きい素数だということです。
素数を掛け合わせることは、コンピューターを使えば、比較的簡単に求められます。上の長い素数同士の掛け算も、コンピューターなら瞬時に計算してしまいます。しかし、ある数を素数に分解する、つまり素因数分解は、コンピューターでも大変な作業なのです。300桁の数を素因数分解するには、コンピューターでも1年間はかかるといいます。2233万桁なら、何万年、いや、もしかしたら何億年もかかるかもしれません(想像もつきません)。
ぼくらは素数を使った暗号で守られている

RSA暗号は、こういう素数の特徴を利用しています。インターネット通信では、まず文字が数字に置き換えられます。先の例でいえば、ぼくがあなたへ送ったメールの文章が数字に変換されます。文字を数字に置き換えるのは簡単な法則で、例えば「あ」は「1」、「い」は「2」という感じになります。
例えば、その方法でぼくのメールが「19715875784567」という数字に置き換えられたとします。このままですと、簡単な法則なのですぐに解読されてしまいます。
そこで、さらにこの数字を、素数を掛け合わせてできた数を使って暗号にします。どうやって暗号にするのかは、とても複雑なので割愛します。例えば上で使った数、「713」のように「素数を掛け合わせた数」が、暗号作成に用いられるわけです。
メールを受け取るあなたのパソコンは、「713」の素となっている「23」と「31」という素数を使って、暗号を元の「19715875784567」という数字に復元し、その数字を「1=あ」、「2=い」という法則に従って文章に戻します。つまり、あなたのパソコンは「23」と「31」という素数を暗号解読の「鍵」にしているわけです。
ぼくのメールが「19715875784567」という数字に置き換えられたことはインターネット上に公開されていますが、「713」という数字を使って暗号化されたことも同時にインターネット上に公開されています。しかし、「713」を「23」と「31」に分解できない限り、暗号は解けません。
「19715875784567」という数字や、「713」という数字が公開されていても、「23」と「31」という素因数分解の鍵が分からない限り、文章を盗み読まれることはないのです。その仕組み上、どうしても情報が公開されてしまうインターネットにおいては、このように素因数分解を鍵にすることはとても便利なのです。
もちろん「713」という数字は小さいですから、すぐ素因数分解されてしまいます。実際には、こんな小さな数は使いません。300桁の数を使えば、暗号解読に1年かかります。1年間は大丈夫。もっともっと大きな素数を使って掛け算をすれば、より安全な暗号ができるというわけです。ぼくらの情報は、このような巨大な素数たちに守られているのです。だから、より大きな素数を発見していくことは、社会的にとても有意義なことなのです。
素数は神秘のベールに包まれている

以下は、素数の神秘についての論考です。どうしても数式や専門用語を使わないと説明できないのですが、あまりそういう所にはとらわれなくても大丈夫です。分からない数式や用語はさらっと流してもらって、全体として言っている内容を読み解いてもらえれば幸いです。
さて、素数は幾つあるのでしょうか。記事に「素数は無限に存在することが証明されている」とあるとおり、無限個です。このことは紀元前300年頃、ユークリッドという学者が証明しています。この証明も長くなるので割愛します。とにかく、「素数は無限個あることが分かっている」と認識してください。暗号づくりには困りませんね。
素数の並び方を見てください。分かりやすいように、素数ではない自然数が間に入る部分を「●」にしてみました。
●2、3●5●7●●●11●13●●●17●19●●●23●●●●●29●31・・・
もちろん、素数はこれだけでなく、この次は37、41、43、47、53・・・と無限に続いていきます。一目瞭然だと思いますが、素数の並び方はバラバラで、何の規則性もないように見えます。2つか3つ進んだだけで次の素数が現れることもあれば、72個も素数に出会わない「素数の砂漠」と呼ばれる場所もあります。
ところが、18世紀初めにオイラーという数学者が驚くべき発見をします。素数を使って、次のような式を考えたのです。無限に続く素数を使った式ですから、この式も無限に続きます。
この式を計算すると、意外な結果が導かれたのです。下記です。
バラバラの並びであると思われていた素数が、このような計算(正確には関数)によって、きれいな数値に収まるのです。しかもπ(パイ…円周率)は、宇宙で最も美しい形である「円」と関係している数です。オイラーは、「素数と宇宙との間には何か密接な関係があるはずだ」と確信したのです。
数学界の難問中の難問、リーマン予想

(写真はピーマン。リーマンの話とは関係ない。単なるダジャレ。)
オイラーの発見から約100年後の19世紀半ば、さらに踏み込んで素数の謎に迫ったのが、リーマンという数学者です。リーマンは、オイラーの式を一般化しました。下記です。
オイラーの式の「2乗」の部分が「m乗」という一般的な記号になっています。リーマンは、この「m」を普通の数ではなく、「複素数」にまで範囲を広げたのです。
複素数とは、実数と虚数でできている数です。実数とは、ぼくらが知っている普通の数です。
虚数とは、2乗したら-1になる数で、「i」と示します。2乗とは、同じ数を2回掛けることです。ですから、2乗したら符号がマイナスになることなんてないはずです。(-1)の2乗だって、「(-1)×(-1)=1」です。だから虚数(うつろな数)というわけです。ちなみに英語では imaginary number(想像上の数)といいます。「i」で表すのは、その頭文字を取っています。
複素数とは、例えば、「3 + 2i」と表します。「3」が実部、「2i」が虚部と呼ばれます。虚数が入った数値なんてイメージできないので、数学の世界では、実部を横軸、虚部を縦軸にして、座標上の点で複素数を視覚化しています。
リーマンが考えた上の式は「ゼータ関数」といいます。このゼータ関数をゼロにする「m」を「ゼロ点」といいます。リーマンは、このゼロ点をいくつか求めて複素数の座標上に落としてみたら、下のような結果を見いだしました。
 ゼロ点は一直線に並びました! 素数の並びは不規則なのですから、ゼータ関数のゼロ点も不規則に現れると思われたのですが、きれいに整列したのです。そこでリーマンは、次のような予想をしました。
ゼロ点は一直線に並びました! 素数の並びは不規則なのですから、ゼータ関数のゼロ点も不規則に現れると思われたのですが、きれいに整列したのです。そこでリーマンは、次のような予想をしました。
「ゼータ関数の自明でないゼロ点は、その実部がすべて1/2の直線上にあるだろう」(1859年)
これを「リーマン予想」といいます。
ちなみに「自明なゼロ点」、つまり数学的には「分かりきっているゼロ点」もあります。「m=-2n」(nは自然数)です。なぜ自明かの説明は省略。
実は、このリーマン予想、未だに証明されていません。多くの数学者が証明を試み、ある学者は精神を病んでしまうほどでした。数学界の難問中の難問なのです。
リーマン予想が証明されたら、宇宙創生の秘密が解明されるかもしれないけど・・・

なぜ、そんなにも一生懸命にリーマン予想を証明しようとしているのかと言えば、この予想は数学というレベルを越えて「宇宙創生の秘密」にまでつながると考えられているからです。
ゼータ関数の自明でないゼロ点が現れる間隔は、次のような式で表されます。
これは、原子核の世界で登場する式とそっくりなのです。原子核のエネルギーは連続ではなく、とびとびになります。そのエネルギーの間隔を表す式は下記のとおりです。
原子核のエネルギー間隔は、物理学の研究によって理論と物証をもって導かれたものです。それが、単なる数学者の遊びにすぎないとも思われるような素数の研究と、まったく同じ結果を示したのです。単なる偶然だと考えるほうが、非科学的です。
自然界の最小単位である素粒子の世界が原子核です。宇宙の基本法則をつかさどるのが素粒子です。そんな素粒子の世界を表現する式と、単なる数字の羅列だと思われていた「素数の並び方」が、密接に関連しているのです! こんなに驚愕する事実が、他にあるでしょうか?
数学は「数を数える」という素朴な行為からスタートしています。「1、2、3、4・・・」と数えるために発明(発見?)されたのが自然数です。その自然数の中に「1とその数自身以外では割り切れない」という「数の基本」ともいえる素数があり、その素数の並び方を研究していくと、上述のように宇宙の基本法則に連結されたのです。
1996年、シアトルにおいて「第1回リーマン予想会議」が開催されました。世界的な数学者・物理学者200人が参加しました。数学上の1つの予想にすぎない事柄について、世界中の学者が会議に集まることから考えてもらえば、リーマン予想の重要性(すなわち、素数の重要性)が分かってもらえるでしょう。その会議では、次のように決議されました。
「リーマン予想と自然法則とのつながりに関する研究は、数学や物理学など、あらゆる分野の学者が共同して挑むべき、人類にとって最も重要な挑戦である。」
参加した数学者たちも、次のように述べています。
ドン・ザキェ博士
「2、3、5、7、11・・・と並ぶ素数の列は、人間の知性を越えた存在であると思えてならない。素数には、この自然の神秘を解き明かす何かが隠されているはずだ。」
ブライアン・コンリー博士
「リーマン予想が証明できれば、我々人類の歴史の1つの時代が終わり、新たな時代が始まるであろう。それは、人類の知性の最高到達点となるはずだ。」
ただし、リーマン予想が証明されると困ったことも起きます。前半で説明したように、現代社会のセキュリティーシステムには、素数による暗号が利用されているからです。不規則な並び方だから暗号として成立するのです。リーマン予想が証明されるということは、素数を生み出す法則が分かるので、どんな素数でも「作ることができる」ということになります。暗号としては役に立たなくなります。
アメリカの国防総省などでは、「リーマン予想を証明した」という論文が発表されると、本当に証明できているかどうかチェックする部署があるほどです。軍事拠点の素数セキュリティーが破られたら大変ですからね。
個人的にはリーマン予想が証明されてほしいなあと思います。だって、宇宙の神秘を知りたいじゃないですか。そもそも、この難問も証明するくらいまで人類の叡智が進歩したときには、既に平和な世界が実現されていて、他人の情報を盗む悪人なんかいなくなっていて、もはや暗号で情報を守る必要なくなるんじゃないかと、ノーテンキに思っています。
こんなに驚愕する事実が、他にあるでしょうか?
すみません。管理主さまの「喜び」が良くわかりません。
端的に言って、「数式が宇宙創成の秘密を解明」できるのかが、今市
ぴんと来ないのです。すみません。
ベッキー&スマップから素数の世界まで、幅広い知識と教養には敬服しています。
あは。すみません。オタク的な喜びとご理解くださいませ。